BOUSSINESQ’S SOLUTION OF VERTICAL STRESSES DUE TO A CONCENTRATED LOAD

In 1885, Boussinesq published equations to determine the state of stress in a subgrade material. He investigated the stresses in a semi-infinite, elastic, isotropic and homogenous solid medium, loaded manually on its upper plane surface by a concentrated point load. The material is also considered weightless and unstressed.

Figure 1. Stresses due to a concentrated load

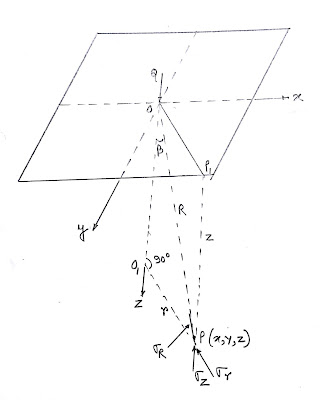
Figure 1 shows a horizontal surface of the elastic continuum subjected to a point load Q at point O. the origin of the coordinates is taken at O. Using logarithmic stress function for the solution of elasticity problem, Boussinesq proved that the polar stress σ_R at point P(x,y,z) is given by-

Where,

R = polar distance between the origin O and point P.

β = angle which the line OP makes with the vertical.

Obviously,

Or,

 Where,

 And,

 And,

 The vertical stress at a point P is given by-

 Where,

The coefficient I_B is known as the Boussinesq influence coefficient for the vertical stress. The values of I_B can be determined for the given value of r/z from the above equation. The computed values are tabulated as shown in the table below.

Table 1. Values of Boussinesq's Coefficient (I_B)

The following points are worth noting when using the above equation:

1. The vertical stress does not depend upon the modulus of elasticity (E) and the Poisson’s ratio (ν). But the solution has been derived assuming that the soil is linearly elastic. The stress distribution will be the same in all linearly elastic materials.

2. The intensity of vertical stress just below the load point is given by-

3. At the surface (z = 0), the vertical stress just below the load is theoretically infinite. However, in an actual case, the soil under the load yields due to a very high stresses. The load point spreads over a small but finite area, and therefore, only finite stresses develop.

4. The vertical stress (σ_z) decreases rapidly with an increase in r/z ratio. Theoretically, the vertical stress would be zero only at an infinite distance from the load point.

5. Boussinesq solution can even be used for negative (upward) loads. For example, if the vertical stress decreases due to an excavation is required, the negative load is equal to the weight of the soil removed. However, as the soil is not fully elastic, the stresses determined are necessarily approximate.

6. The field measurements indicate that the actual stresses are generally smaller than the theoretical values given by Boussinesq’s solution at shallow depths. Thus, the Boussinesq solution gives conservative values and is commonly used in soil engineering problems.

Limitations of Boussinesq’s Solution:

1. The solution was initially obtained for determination of stresses in elastic solids. Its application to solids may be questioned, as the solids are far from purely elastic solids.

2. The application of Boussinesq’s solution can be justified when the stresses changes are such that only a stress increase occurs in the soil. The real requirement for use of the solution is not that the soil be elastic (i.e. fully recoverable), but it should have a constant ratio between stress and strain. When the stress decrease occurs, the relation between stress and strain is not linear and, therefore, the solution is not strictly applicable. If the stresses included in the soil are small in comparison with the shear strength of the soil, the soil behaves somewhat elastically and the Boussinesq solution can be used.

3. For practical cases, the Boussinesq solution can be safely used for homogenous deposits of clay, man-made fills and for limited thickness of uniform sand deposits. In deep sand deposits, the modulus of elasticity increases with an increase in depth and, therefore, the Boussinesq solution will not give satisfactory results. In this case, the assumption of proportionality between stress and strain cannot be justified. For such a case, non-linear elastic solutions or elastic-plastic solutions are required.

4. The point load applied below ground surface cause somewhat smaller stresses than are caused by surface loads, and therefore, the Boussinesq solution is not strictly applicable. However, the solution is frequently used for shallow footings, in which z is measured below the base of the footing.